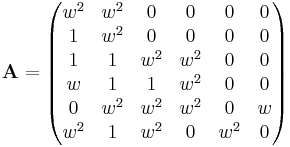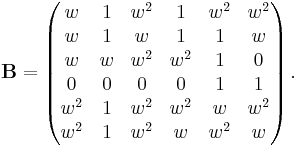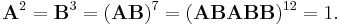Hall–Janko group

Group theory

Group theory
Basic notions Subgroup Normal subgroup Quotient group Group homomorphism (semi-)direct product
Finite groups (classification) Cyclic group Z_n Symmetric group, S_n Dihedral group, D_n Alternating group A_n Mathieu groups M₁₁, M₁₂, M₂₂, M₂₃, M₂₄ Conway groups Co₁, Co₂, Co₃ Janko groups J₁, J₂, J₃, J₄ Fischer groups F₂₂, F₂₃, F₂₄ Baby Monster group B Monster group M
Discrete groups and lattices The integers, Z Lattice (group) Modular groups, PSL(2,Z) and SL(2,Z)
Topological groups and Lie groups Solenoid (mathematics) Circle group General linear group GL(n) Special linear group SL(n) Orthogonal group O(n) Special orthogonal group SO(n) Unitary group U(n) Special unitary group SU(n) Symplectic group Sp(n) G₂ F₄ E₆ E₇ E₈ Lorentz group Poincaré group Conformal group Diffeomorphism group Loop group Infinite-dimensional Lie groups O(∞) SU(∞) Sp(∞)

In mathematics, the Hall-Janko group HJ, is a finite simple sporadic group of order 604800. It is also called the second Janko group J₂, or the Hall-Janko-Wales group, since it was predicted by Janko and constructed by Hall and Wales. It is a subgroup of index two of the group of automorphisms of the Hall-Janko graph, leading to a permutation representation of degree 100.

It has a modular representation of dimension six over the field of four elements; if in characteristic two we have w² + w + 1 = 0, then J₂ is generated by the two matrices

${\mathbf A} = \left ( \begin{matrix} w^2 & w^2 & 0 & 0 & 0 & 0 \\ 1 & w^2 & 0 & 0 & 0 & 0 \\ 1 & 1 & w^2 & w^2 & 0 & 0 \\ w & 1 & 1 & w^2 & 0 & 0 \\ 0 & w^2 & w^2 & w^2 & 0 & w \\ w^2 & 1 & w^2 & 0 & w^2 & 0 \end{matrix} \right )$

and

${\mathbf B} = \left ( \begin{matrix} w & 1 & w^2 & 1 & w^2 & w^2 \\ w & 1 & w & 1 & 1 & w \\ w & w & w^2 & w^2 & 1 & 0 \\ 0 & 0 & 0 & 0 & 1 & 1 \\ w^2 & 1 & w^2 & w^2 & w & w^2 \\ w^2 & 1 & w^2 & w & w^2 & w \end{matrix} \right ).$

These matrices satisfy the equations

${\mathbf A}^2 = {\mathbf B}^3 = ({\mathbf A}{\mathbf B})^7 = ({\mathbf A}{\mathbf B}{\mathbf A}{\mathbf B}{\mathbf B})^{12} = 1.$

J₂ is thus a Hurwitz group, a finite homomorphic image of the (2,3,7) triangle group.

The matrix representation given above constitutes an embedding into Dickson's group G₂(4). There are two conjugacy classes of HJ in G₂(4), and they are equivalent under the automorphism on the field F₄. Their intersection (the "real" subgroup) is simple of order 6048. G₂(4) is in turn isomorphic to a subgroup of the Conway group Co₁.

J₂ is the only one of the 4 Janko groups that is a section of the Monster group; it is thus part of what Robert Griess calls the Happy Family. Since it is also found in the Conway group Co₁, it is therefore part of the second generation of the Happy Family.

Griess relates [p. 123] how Marshall Hall, as editor of The Journal of Algebra, received a very short paper entitled "A simple group of order 604801." Yes, 604801 is prime.

J₂ has 9 conjugacy classes of maximal subgroups. Some are here described in terms of action on the Hall-Janko graph.

U₃(3) order 6048 - one-point stabilizer, with orbits of 36 and 63

Simple, containing 36 simple subgroups of order 168 and 63 involutions, all conjugate, each moving 80 points. A given involution is found in 12 168-subgroups, thus fixes them under conjugacy. Its centralizer has structure 4.S₄, which contains 6 additional involutions.

3.PGL(2,9) order 2160 - has a subquotient A₆

2¹⁺⁴:A₅ order 1920 - centralizer of involution moving 80 points

2²⁺⁴:(3 × S₃) order 1152

A₄ × A₅ order 720

Containing 2² × A₅ (order 240), centralizer of 3 involutions each moving 100 points

A₅ × D₁₀ order 600

PGL(2,7) order 336

5²:D₁₂ order 300

A₅ order 60

Janko predicted both J₂ and J₃ as simple groups having 2¹⁺⁴:A₅ as a centralizer of an involution.

Number of elements of each order

The maximum order of any element is 15. As permutations, elements act on the 100 vertices of the Hall-Janko graph.

Order	No. elements	Cycle structure and conjugacy
1 = 1	1 = 1	1 class
2 = 2	315 = 3² · 5 · 7	2⁴⁰, 1 class
2 = 2	2520 = 2³ · 3² · 5 · 7	2⁵⁰, 1 class
3 = 3	560 = 2⁴ · 5 · 7	3³⁰, 1 class
3 = 3	16800 = 2⁵ · 3 · 5² · 7	3³², 1 class
4 = 2²	6300 = 2² · 3² · 5² · 7	2⁶4²⁰, 1 class
5 = 5	4032 = 2⁶ · 3² · 7	5²⁰, 2 classes, power equivalent
5 = 5	24192 = 2⁷ · 3³ · 7	5²⁰, 2 classes, power equivalent
6 = 2 · 3	25200 = 2⁴ · 3² · 5² · 7	2⁴3⁶6¹², 1 class
6 = 2 · 3	50400 = 2⁵ · 3² · 5² · 7	2²6¹⁶, 1 class
7 = 7	86400 = 2⁷ · 3³ · 5²	7¹⁴, 1 class
8 = 2³	75600 = 2⁴ · 3³ · 5² · 7	2³4³8¹⁰, 1 class
10 = 2 · 5	60480 = 2⁶ · 3³ · 5 · 7	10¹⁰, 2 classes, power equivalent
10 = 2 · 5	120960 = 2⁷ · 3³ · 5 · 7	5⁴10⁸, 2 classes, power equivalent
12 = 2² · 3	50400 = 2⁵ · 3² · 5² · 7	3²4²6²12⁶, 1 class
15 = 3 · 5	80640 = 2⁸ · 3² · 5 · 7	5²15⁶, 2 classes, power equivalent

References

Robert L. Griess, Jr., "Twelve Sporadic Groups", Springer-Verlag, 1998.
Marshall Hall, Jr. and David Wales, "The Simple Group of Order 604,800", Journal of Algebra, 9 (1968), 417-450.
Wales, David B., "The uniqueness of the simple group of order 604800 as a subgroup of SL(6,4)", Journal of Algebra 11 (1969), 455 - 460.
Wales, David B., "Generators of the Hall-Janko group as a subgroup of G2(4)", Journal of Algebra 13 (1969), 513–516, doi:10.1016/0021-8693(69)90113-6, MR0251133, ISSN 0021-8693
Z. Janko, Some new finite simple groups of finite order, 1969 Symposia Mathematica (INDAM, Rome, 1967/68), Vol. 1 pp. 25-64 Academic Press, London MR 0244371
Atlas of Finite Group Representations: J₂